Portfolio Optimization tool using TD3 RL Algorithm!
Overview
Over the course of this spring semester I've been a little busy being a apart of the Minutemen Alternative Investment Fund's freshman Quant program called ARQ. In ARQ I've had the pleasure of meeting a lot of brilliant people, all of which are realllly cracked, imposter syndrome took a little while to calm down. The main purpose of this post however is mainly to detail the recent project that I've been working on as a part of ARQ. My pitch group was tasked with researching and implementing our very own strategy from scratch, and that's what we did!
Abstract
What we ended up coming up with at first was a simple "Delta-Neutral" Portfolio Optimization tool that aimed to optimize your portfolio by adjusting the weight you're currently invested in a single asset based off it's delta value. The idea behind this originally was to have an average Delta across all the assets in your portfolio as close to zero as possible with a goal of being risk-adverse. The main issue that came with this however was the fact that with a Delta closer and closer to 0 you would be making less and less money with each underlying price movement. Obviously this is super counter-intuitive as the point of owning a stock is to make some sort of profit off it. So we went back to the drawing board...
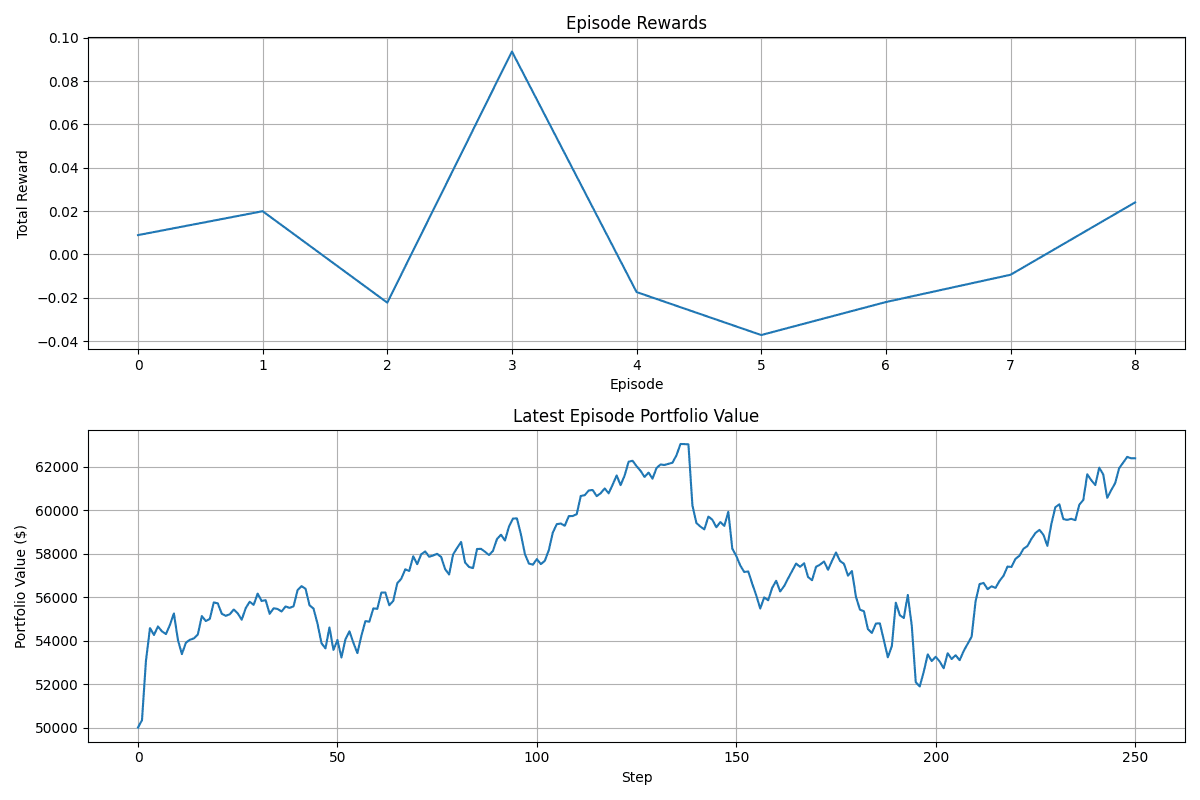
It was with the help of the current Co-head of MAIF's quant arm, Mason Choi, that we were able to iterate on our idea and come up with a cool tool that could work in a real-life setting. The plan was to keep the portfolio optimization idea and being risk-adverse but straying away from Delta as a whole. We instead aimed to essentially maximize the sharpe ratio of our portfolio as much as possible utilizing reinforcement learning and portfolio weight allocation. The specific RL algorithm I implemented was the TD3 algorithm that is centered around a single Actor network and two Critic networks. The Actor network would take in as inputs the current state space (our portfolio) and an action (the current portfolio weights). It would then propose an action to take for our two Critic networks to then evaluate, this action would be the re-allocation of the portfolio weights based on stock performance. The two Critics would then evaluate the inputs and come up with an output based on the state and action provided, our TD3 agent would take the minimum of those two! This same process would then be looped over a course of 252 days, or one fiscal year, resulting in our first episode being complete!
The code
My role within this project was to be one of the Quantitative Developers, I focused on constructing our trading environment for out TD3 agent to exist in and built the classes for our TD3 Agent along with our Actor and Critic networks from the ground up. The cool part about all of this was honestly the fact that I really sat down and forced myself to learn through all of this random documentation and got around to building something tangible with everything included. It was interesting to see for the first part about how a "trading environment" is really simple and just represented as an abstract data type with specific methods and attributes that our TD3 Agent could iterate on. I'll include the general constructor of the our Market_env class but it's crazy to think that something so powerful is built on something so simple
def __init__(self, stock_data, transaction_cost=0.001, risk_free_rate=0.02/252):
super(MarketEnv, self).__init__()
self.stock_data = stock_data # full price data of our stock universe
self.n_stocks = stock_data.shape[1]
self.starting_cash = 50000 # Example/Placeholder
self.transaction_cost = transaction_cost
self.risk_free_rate = risk_free_rate
# Define action and observation spaces
self.action_space = spaces.Box(
low=0, high=1, shape=(self.n_stocks,), dtype=np.float32
)
self.observation_space = spaces.Box(
low=-np.inf, high=np.inf, shape=(self.n_stocks,), dtype=np.float32
)
self.reset()
There's a couple of things included mainly meant to help me create some helper functions later on like sharpe ratio calculations, etc, but the main thing I want to point attention to is our Action and State observation spaces! These are exactly what end up being passed into our TD3 Agent eventually to then be processed by our Actor and Critic Networks!
Another super cool part about all of this is really the actual data pipeline for our TD3 Agent! To maintain brevity I won't dive into all of the theory behind the TD3 algo but what I will explain is how the state and action actually affect our Agent.
TD3 Pipeline
The main benefit of TD3 is it's stability within continuous spaces, it's originally derived from the DDPG algorithm which was great when used in continuous spaces but lacked support against discrete values. The TD3 algo addresses this issue with the use of an actor-critic network and tackling overfitting bias and instability! It first learns some policy, this is going to be our actor, that then maps states to actions. We then have two Q-functions, which we address as our critics, to estimate the expected return from the state, action pair. We then integrate target networks (delayed, slowly updated copies of the actor and critics) to improve our stability.
This looks like:
self.actor = actor
self.actor_target = Actor(state_dim, action_dim)
self.actor_target.load_state_dict(self.actor.state_dict())
self.critic_1 = critic
self.critic_target_1 = Critic(state_dim, action_dim)
self.critic_target_1.load_state_dict(self.critic_1.state_dict())
self.critic_2 = Critic(state_dim, action_dim)
self.critic_target_2 = Critic(state_dim, action_dim)
self.critic_target_2.load_state_dict(self.critic_2.state_dict())
The first checkpoint we reach is where we collect experience:
- The agent interacts with the environment:
- At time t, it'll observe the current state
- It'll then select an action
- Then the environment will return the next state, action, reward, and a done flag to store in a replay buffer. Our next goal is to sample a random minibatch of transitions from the replay buffer, this is another function I've created(see below)
class ReplayBuffer:
def __init__(self, state_dim, action_dim, max_size = int(2e5)):
self.max_size = max_size
self.ptr = 0
self.size = 0
self.state = np.zeros((max_size, state_dim))
self.action = np.zeros((max_size, action_dim))
self.reward = np.zeros((max_size, 1))
self.next_state = np.zeros((max_size, state_dim))
self.done = np.zeros((max_size, 1))
def add(self, state, action, reward, next_state, done):
self.state[self.ptr] = state
self.action[self.ptr] = action
self.reward[self.ptr] = reward
self.next_state[self.ptr] = next_state
self.done[self.ptr] = done
self.ptr = (self.ptr + 1) % self.max_size
self.size = min(self.size +1, self.max_size)
def sample(self, batch_size):
idxs = np.random.randint(0, self.size, size=batch_size)
return (
self.state[idxs],
self.action[idxs],
self.reward[idxs],
self.next_state[idxs],
self.done[idxs]
)
We'll then use our target actor network to get the next action which is computed using our next state added with some clipped noise function. The noise regularizes the target and avoids overfitting to deterministic next actions.
We deploy target critics to compute the target Q value, then taking the minimum of the two Q-values to reduce the overestimation bias, again aiming to avoid overfitting.
Our next step is to update the two critics by minimizing our downside. As we iterate the critics learn, eventually, to estimate how good a given state-action pair is. Every d steps (every 2 critic updates normally) we update the actor. The actor aims to maximize the q value predicted by the one critic, essentially learning to choose better actions in every state.
Over time we soft update the target networks using some type of averaging (polyak in our case), we need to do this because the actor and critic updates would chase each other too aggressively, causing divergence without targets to hit. The targets effectively slow down the target value changes, making the critics targets more stable leading to more stable and robust learning!
Conclusion
Yeah so I had a lot of fun working on this one, especially considering I never really had the chance to work alongside people before on a project like this. 10/10 would recommend!
Anyway, thanks for reading again peace!
-Vic
